Table of Continuous time Pulsation Fourier Transform Pairs
3.2.1. The Fourier Transform¶
Now we consider functions \(x(t)\) that are not (necessarily) periodic. In this case there is no such thing as a fundamental period and fundamental frequency. Therefore there are no harmonics and it proves that we need exponentials of all frequencies to syntesize the signal \(x(t)\):
\[x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\w)e^{j\w t}d\omega\]
We see that \(X(\w)\) determines the weight (relative importance) of the exponential function \(\exp(j\w t)\) in the synthesis of the signal \(x(t)\). That function \(X(\w)\) is called the Fourier transform of \(x(t)\) and will denoted by \(X(\w) = \FT(x(t))\)
We will often write:
\[x(t) \xrightarrow{\quad\FT\quad} X(\w)\]
The Fourier transform (the analysis equation) is given by
\[X(\w) = \int_{-\infty}^{\infty} x(t) e^{-j\w t} dt\]
As there is a one to one correspondence between a signal we can also write:
\[x(t) \xleftarrow{\quad\IFT\quad} X(\w)\quad\text{or}\quad X(\w) \xrightarrow{\quad\IFT\quad} x(t)\]
This arrow diagram evidently refers to the inverse Fourier transform or the synthesis equation.
3.2.2. Properties of the CT Fourier Transform¶
First we present some of the properties of the Fourier transform. In later sections we will provide some proofs and some uses and consequences of these properties.
| Time Domain | Frequency Domain |
|---|---|
| Synthesis (Inverse Fourier Transform) \[x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\w)e^{j\w t}d\omega\] | Analysis (Fourier Transform) \[X(\w) = \int_{-\infty}^{\infty} x(t) e^{-j\w t} dt\] |
| Real Signals \[x(t) \in\setR\] | Symmetry in Fourier transform \[X(-\w) = X^\star(\w)\] |
| Even Signals \[x(-t) = x(t)\] | Real Fourier transform \[X(\w) \text{ is real and even}\] |
| Odd Signals \[x(-t) = -x(t)\] | Imaginary Fourier transform \[X(\w) \text{ is imaginary and odd}\] |
| Derivative \[x'(t) = \frac{d}{dt} x(t)\] | High frequency gain \[j\w X(\w)\] |
| Time scaling \[x(a t)\] | Frequency scaling \[\frac{1}{|a|}X(\frac{\w}{a})\] |
| Convolution \[x(t) \ast y(t) = \int_{-\infty}^{\infty} x(t-u) y(u) du\] | Multiplication \[X(\w) Y(\w)\] |
| Multiplication \[x(t) y(t)\] | Convolution \[\frac{1}{2\pi} X(\w) \ast Y(\w)\] |
| Duality \[\begin{split}x(t)\\ X(t)\end{split}\] | \(\hspace{1em}\) \[\begin{split}X(\w)\\ 2\pi x(-\w)\end{split}\] |
3.2.2.1. Real Signals¶
Let \(x(t)\) be a real valued signal. For the Fourier transform \(X(\w)\) we can write:
\[\begin{split}X(\w) &= \int_{-\infty}^{\infty} x(t)\left(\cos(\w t)- j \sin(\w t)\right)dt\\ &= \int_{-\infty}^{\infty} x(t)\cos(\w t)dt - j\int_{-\infty}^{\infty} x(t)\sin(\w t)dt\end{split}\]
For \(X(-\w)\) we get
\[\begin{split}X(-\w) &= \int_{-\infty}^{\infty} x(t)\left(\cos(\w t) + j \sin(\w t)\right)dt\\ &= \int_{-\infty}^{\infty} x(t)\cos(\w t)dt + j\int_{-\infty}^{\infty} x(t)\sin(\w t)dt\end{split}\]
Showing that \(X(-\w) = X^\star(\w)\). The consequence of this symmetry in the Fourier transform is that when plotting the Fourier transform we only have to consider the positive frequencies.
3.2.2.2. Even and Odd Signals¶
We start by rewriting the definition of the Fourier transform:
\[\begin{split}X(\w) &= \int_{-\infty}^{\infty} x(t)e^{-j\w t}dt\\ &= \int_{-\infty}^{0} x(t)e^{-j\w t}dt + \int_{0}^{\infty} x(t)e^{-j\w t}dt\\ &= \int_{0}^{\infty} x(-t)e^{j\w t}dt + \int_{0}^{\infty} x(t)e^{-j\w t}dt\end{split}\]
For an even signal we have \(x(-t)=x(t)\) and thus
\[\begin{split}X(\w) &= \int_{0}^{\infty} x(t)e^{j\w t}dt + \int_{0}^{\infty} x(t)e^{-j\w t}dt\\ &= \int_{0}^{\infty} x(t)\left( e^{j\w t}+e^{-jwt} \right)\\ &= 2 \int_{0}^{\infty} x(t)\cos(\w t) dt\end{split}\]
For a real and even signal we see that the Fourier transform is real valued. Furthermore \(X(\w)\) is an even function (note that the product of two even functions (\(x(t)\) and \(\cos(\w t)\) is even too).
Along the same line of reasoning it can be shown that the Fourier transform of an odd signal is purely imaginairy and odd.
3.2.2.3. Derivatives¶
Let
\[x(t) \FTright X(\w)\]
then:
\[x'(t) \FTright j\w X(\w)\]
The proof simply follows from the synthesis equation:
\[x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\w) e^{j\w t}dw\]
Differentiating with respect to \(t\) on both sides of the equation and using Leibnitz integration rule we get
\[\begin{split}x'(t) &= \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\w) \frac{d}{dt}e^{j\w t}dw\\ &= \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\w) j\w e^{j\w t}dw\end{split}\]
From this equation we see that \(j \w X(\w)\) is the Fourier transform of \(x'(t)\).
3.2.2.4. Pulse Function¶
Let \(x(t)=\delta(t)\), this pulse function 'contains' all frequencies in a equal amount, i.e. \(X(\w)=1\). This is evidently true given the sieve property of a pulse function.
\[\delta(t) \FTright 1\]
For a shifted pulse we have
\[\delta(t-t_0) \FTright e^{-j\w t_0}\]
3.2.2.5. Time Shifts¶
The Fourier transform of a shifted function \(y(t) = x(t-t_0)\) is:
\[\begin{split}Y(\w) &= \int_{-\infty}^{\infty} y(t)e^{-j\w t} dt\\ &= \int_{-\infty}^{\infty} x(t-t_0) e^{-j\w t} dt\end{split}\]
changing to variable \(t' = t - t_0\) we get:
\[\begin{split}Y(\w) &= \int_{-\infty}^{\infty} x(t') e^{-j\w (t'+t_0)} dt'\\ &= e^{-j\w t_0} \int_{-\infty}^{\infty} x(t') e^{-j\w t'} dt'\\ &= e^{-j\w t_0} X(\w)\end{split}\]
So
\[x(t-t_0) \FTright e^{-j\w t_0} X(\w)\]
3.2.2.6. Complex Exponential¶
A complex exponential function \(x(t)=e^{j\w_0 t}\) contains just one frequency \(\w_0\) so its Fourier transform be a pulse at that frequency. And indeed we can prove:
\[e^{j\w_0 t} \FTright 2\pi \delta(w-\w_0)\]
If you start in the time domain and use the Fourier transform you end up with the need to prove that:
\[\int_{-\infty}^{\infty} e^{j (w-w_0) t} dt\]
is a pulse at \(w_0\). It is simpler in this case to start with the pulse in the frequency domain and calculate its inverse Fourier transform:
\[\frac{1}{2\pi} \int_{-\infty}^{\infty} 2\pi \delta(\w - \w_0) e^{j\w t} d\w = e^{j\w_0 t}\]
3.2.2.7. Periodic Signal¶
Let \(x(t)\) be a periodic signal, i.e. \(x(t+T_0)=x(t)\) then we calculate the Fourier Series coefficients \(a_k\) and write:
\[x(t) = \sum_{k=-\infty}^{\infty} a_k e^{j k \w_0 t}\]
where \(\w_0 = 2\pi/T_0\). This expression for \(x(t)\) can be used to calculate the Fourier transform (not the series coefficients) of \(x(t)\):
\[\begin{split}X(\w) &= \int_{-\infty}^{\infty} x(t) e^{-j\w t} dt\\ &= \int_{-\infty}^{\infty} \left( \sum_{k=-\infty}^{\infty} a_k e^{j k \w_0 t} \right) e^{-j\w t} dt\\\end{split}\]
Interchanging sum and integration
\[X(\w) = \sum_{k=-\infty}^{\infty} a_k \int_{-\infty}^{\infty} e^{j k \w_0 t} e^{-j\w t} dt\]
where the integral is the Fourier transform of \(e^{jk\w_0 t}\) which was shown to be \(2\pi \delta(\w-k\w_0)\) and so:
\[X(\w) = 2\pi \sum_{k=-\infty}^{\infty} a_k \delta(\w-k\w_0)\]
showing that the Fourier transform of a periodic function is a modulated pulse train. The energy in the pulse at \(\w=k \w_0\) is equal to \(2\pi a_k\).
3.2.2.8. Pulse Train¶
Consider the pulse train
\[x(t) = \sum_{k=-\infty}^{\infty} \delta(t - kT_0)\]
Somewhat suprisingly its Fourier transform is a pulse train as well:
\[X(\w) = \w_0 \sum_{k=-\infty}^{\infty} \delta(\w-k\w_0)\]
The proof is easy when you realize that the pulse train is a periodic function with period \(T_0\). For this periodic function we can calculate the Fourier coefficients \(a_k\):
\[\begin{split}a_k &= \frac{1}{T_0} \int_{-T_0/2}^{T_0/2} \delta(t) e^{-j k\w_0 t}dt\\ &= \frac{1}{T_0}\end{split}\]
(remember the sieve property of the delta function?). Now we can use the result for any periodic function and substitute the \(a_k\) for the pulse train:
\[\begin{split}X(\w) &= 2\pi \sum_{k=-\infty}^{\infty} a_k \delta(\w-k\w_0)\\ &= \frac{2\pi}{T_0} \sum_{k=-\infty}^{\infty} \delta(\w-k\w_0)\\ &= \w_0 \sum_{k=-\infty}^{\infty} \delta(\w-k\w_0)\end{split}\]
3.2.2.9. Convolution¶
Given two signal \(x(t)\) and \(y(t)\) with Fourier transforms \(X(\w)\) and \(Y(\w)\) respectively. Then
\[\begin{split}x(t) \ast y(t) &\FTright X(\w)Y(\w)\\ x(t)y(t) &\FTright \frac{1}{2\pi} X(\w) \ast Y(\w)\end{split}\]
3.2.3. Duality¶
Todo
Duality of the CT Fourier Transform
3.2.4. Fourier Transform Pairs¶
First we present some basic and often needed Fourier transform pairs. Proofs of some of these pairs will be given later on.
| Time Domain | Frequency Domain |
|---|---|
| Synthesis \[x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\w)e^{j\w t}d\omega\] | Analysis \[X(\w) = \int_{-\infty}^{\infty} x(t) e^{-j\w t} dt\] |
| Pulse \[x(t) = \delta(t)\] | Constant \[X(\w) = 1\] |
| Finite Pulse \[\begin{split}x(t) = \begin{cases} 1/2 &: -1 \leq x \leq 1\\ 0 &: \text{elsewhere} \end{cases}\end{split}\] | Sinc \[X(\w) = \frac{\sin(\w)}{\w}\] |
| Complex Exponential \[e^{j\w_0 t}\] | Pulse \[2\pi \delta(\w-\w_0)\] |
| Cosine \[\cos(\w_0 t)\] | Pulses \[\pi( \delta(\w-\w_0) + \delta(\w+\w_0) )\] |
| Sine \[\sin(\w_0 t)\] | Pulses \[\frac{\pi}{j} (\delta(\w-\w_0) - \delta(\w+\w_0) )\] |
| Pulse train \[\sum_{n=-\infty}^{\infty} \delta(t - nT)\] | Pulse train \[\frac{2\pi}{T} \sum_{k=-\infty}^{\infty} \delta\left( \w - \frac{2\pi k}{T}\right)\] |
3.2.5. Exercises¶
-
- Odd Signals
-
Give a proof that the Fourier transform \(X(\w)\) of a real and odd signal \(x(t)\) is purely imaginairy.
-
- Finite Pulse Signal
-
Give a proof that the Fourier transfor of the pulse function:
\[\begin{split}x(t) = \begin{cases} 1/2 &: -1 \leq x \leq 1\\ 0 &: \text{elsewhere} \end{cases}\end{split}\]
is given by
\[X(\w) = \frac{\sin\w}{\w}\]
-
- Sine and Cosine
-
Calculate the Fourier transform of \(\sin(\w t)\) and \(\cos(\w t)\). The anwers are not enough (these are in the table above), you should give a proof.
-
- Impulse response
-
Calculate the Fourier transform \(H(\w)\) of the function \(h(t)\),
\[h(t) = e^{-t} u(t)\]
where \(u(t)\) is the step function.
-
- Linear System Response
-
The function \(h(t)\) is the impulse response function of a linear system that is known as a low pass filter.
-
Make a Bode plot of \(H(\w)\) (i.e. on logarithmic scales) and show that frequencies below \(\w=1\) are passed unchanged by this filter whereas frequencies above \(\w=1\) are decreased in amplitude.
-
Consider the signal:
\[x(t) = 5 \sin(0.5t) + \sin(2 t)\]
Plot this signal. You see a low frequency sinusoid of large amplitude with a high frequency small ampliture sinusoid added to it.
-
Calculate the Fourier transform \(X(\w)\) of \(x(t)\).
-
The linear system characterized with impulse response \(h(t)\) is fed with input signal \(x(t)\) to produce output signal \(y(t)\). Calculate \(y(t)\). Hint: use the convolution property of the Fourier transform.
Plot \(x(t)\) and \(y(t)\) in the same figure.
-
-
- Finite Width Impulse \(\FTright\) Sinc
-
Consider the finite width pulse function:
\[\begin{split}x_a(t) = \begin{cases} 1/(2a) &: -a \leq x \leq a\\ 0 &: \text{elsewhere} \end{cases}\end{split}\]
Calculate the Fourier transform \(X_a(\w)\) and plot both \(x_a(t)\) and \(X_a(\w)\) for \(a=1,2,3\).
-
- Convolution
-
Give a proof of the convolution property:
\[x(t)\ast y(t) \FTright X(\w)Y(\w)\]
The most elegant proof will be presented in the lecture notes for future students.
-
- Example
-
Consider the real valued, even function \(x(t)\) whose Fourier spectrum \(|X(\w)|\) is
\[\begin{split}|X(\w)| = \begin{cases} 1 - \frac{\w}{\w_0} &: 0\leq\w<\w_0\\ 0 &: \w \geq \w_0 \end{cases}\end{split}\]
and is sketched in the figure below (with \(\w_0=2\))
Show code for figure
1 import numpy as np 2 import matplotlib.pyplot as plt 3 4 plt . clf () 5 6 w0 = 2 7 w = np . linspace ( 0 , 6 , 100 ) 8 X = np . maximum ( 0 , 1 - w / w0 ) 9 10 plt . gcf () . set_size_inches ( 5 , 3 ) 11 plt . plot ( w , X ) 12 plt . savefig ( 'source/figures/Xexample.png' )
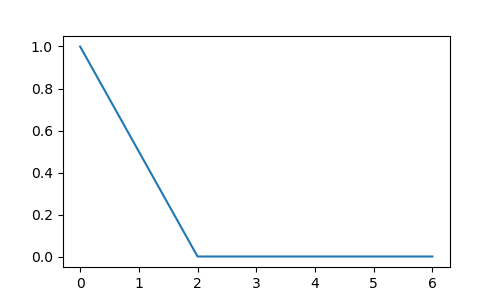
The Fourier spectrum is only given for the positive \(\w\) values, the rest follows from symmetry principles.
-
Sketch the spectrum \(|X(\w)|\) for all \(\w\).
-
What is the Fourier transform \(X(\w)\)? Also give a sketch.
-
Calculate and plot the signal \(x(t)\). If your integral calculation skills are a bit rusty you can use Mathematica (Wolfram Alpha) or Maple or …
-
Source: https://staff.fnwi.uva.nl/r.vandenboomgaard/SignalProcessing/FrequencyDomain/CTNP.html
0 Response to "Table of Continuous time Pulsation Fourier Transform Pairs"
Post a Comment